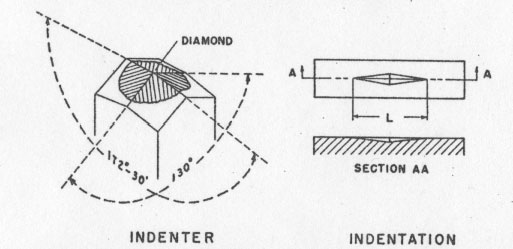
Volume 30, pages 583-595, 1945

     THE KNOOP MICROHARDNESS TESTER AS A MINERALOGICAL TOOL¹

     HORACE WINCHELL²

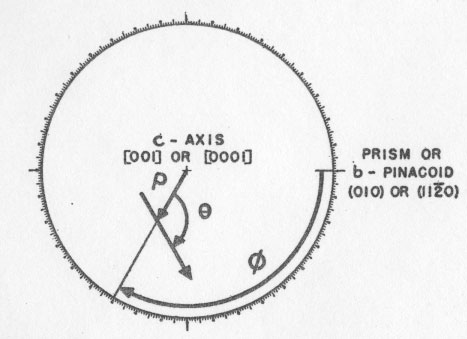
     I=W/L²c

     I=Knoop hardness number.

     W=Load applied to the indenter, in kilograms.

     L=Length of the indentation, originally defined as in centimeters; but L may be measured in any length units desired and the conversion factor to centimeters may be included in c.

     c=a constant depending upon the shape of the indenter. It may also include conversion factors depending upon the units actually used to measure W and L.

     As stated above, the equation may be expressed by straight lines, one for each applicable load, on logarithmic graph paper. The scale of the graph may be made such that there will be no danger of introducing errors that are larger than probable errors inherent in the measurement of the indentation by optical methods.

     The form of the above equation shows that to achieve a given relative or percentage accuracy in I, L must be measured with a maximum relative or percentage error one-half as great. For example, if L is measured with an error of 1 part in 100, the resulting error in I would be 2 parts in 100.

     RELIABILITY

     To evaluate the accuracy or consistency of the Tukon tester in the laboratories of the Hamilton Watch Company, for mineral testing purposes, several specimens were tested many times each. The results will be found summarized and expressed as probable error³ in Table 2. It was found that most hardness readings will be repeated within about 2 to 5 per cent of the average, when many indentations are made in the same orientation on the same crystal surface. The probable error of an observation or of the average of several observations is appreciably increased if any of the observations are made on indentations associated with cracks or other fractures. In accordance with logical arguments that the highest reading will be obtained with the least fracturing, it was concluded that the maximum of a series of readings should be selected if fractures appear with any of them; but the average should be considered the best value if no fractures occurred. According to that convention, the best value is indicated in Table 2 in boldface.

     A note of caution must be included here regarding these measures of accuracy. The "probable error" shown in Table 2 and defined above is really a measure of the self-consistency of the given set of observations. It takes no account of possible systematic errors such as the dependence of the hardness number upon the load on the indenter (Tate, 1944), or imperfectly shaped or polished indenters. "Probable errors" also do not include errors due to faulty specimen preparation (polishing, levelling, etc.) or improper adjustment of the Tukon testing machine. Our efforts were mainly to control such variables by holding them constant. We have made no attempt to determine the importance of such factors for this study. Another still undetermined source of possible error is the crystallographic orientation of the diamond indenter. So far as is known, the makers of the indenters do not attempt to hold this constant. This factor would undoubtedly be negligible for soft and medium specimens but in testing materials of great hardness, the elastic properties and hardness of the diamond itself would be of the same order of magnitude as those of the specimen, and should therefore be considered. It is our impression that such properties would vary appreciably with the orientation of the diamond.

     For all these reasons, then, the reader is cautioned not to accept uncritically the fourth, nor even the third significant figures of the hardness numbers quoted in Table 2. The probable error alone (2% to 5%) would generally indicate that the fourth digit can have little significance. Nevertheless, until full information on validity of results is available from all sources, it seems best not to round off the numbers farther than to the nearest 5 units in the fourth significant figure. This consideration probably would not affect results for soft materials, but might noticeably affect those reported for materials of greater hardness than 1000.

     SPECIFICATION OF ORIENTATION

     To correlate hardness numbers with orientation of the test surface and of the long axis of the indenter in that surface, three independent coordinate angles are necessary. These angles may be compared with longitude, colatitude, and azimuth or bearing on the surface of the earth. The two-circle goniometer studies of Goldschmidt, Palache, and others (Dana-Palache et al. 1944, pp. 3-37) form the basis for the definition of the orientation coordinates of the surface tested:

     "longitude" =phi (φ)

     "colatitude" or polar distance= rho (ρ).

     The azimuth or bearing, designated theta (θ), is measured clockwise from the north or meridian direction to the long axis of the indenter. Figure 3 shows these angles in stereographic projection. Phi (φ) is measured clockwise about the fundamental circle of the projection from the point representing the plane (010) or (110). Rho (p) is the polar angle, measured radially outward from the center of the projection (the point representing the axis of the prism zone). And theta (θ) is measured clockwise about the point representing the test plane. These definitions serve for all points except the pole of the sphere (ρ=0°). At this point, θ must be defined specially, as the direction-angle measured like φ around the fundamental circle.

    
FIG. 3. Stereographic projection illustrating the definitions of φ, ρ, θ, the angular coordinates of the test surface and of the long axis of the indentation therein, taken with respect to conventional crystal axes of any system. For the orientation ρ=0°, φ is indeterminate and θ is specially defined as the direction-angle, measured around the fundamental circle normally used for φ.

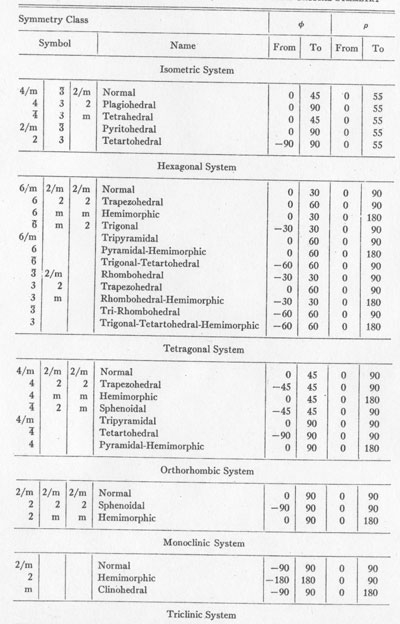
     It will be evident that these definitions permit choosing the following ranges for the three coordinate angles:

     -180° <   φ  <=180°
           0° <= ρ  <=180° 
           0° <= θ   < 360°

     However, φ and ρ may be limited to smaller values by taking into consideration the symmetry of the applicable crystal class, as shown in Table 1. Also θ may be limited to smaller values by the twofold symmetry axis of the indenter itself, and also to special values if the test plane is normal to certain symmetry planes or to an axis of higher symmetry in the crystal. In general, 0° <= θ < 180°, because of the symmetry of the indenter only.

     Graphical calculations leading to the expression of the coordinates are not difficult for most crystals. They are most easily carried out by means of gnomonic or stereographic projections based upon Laue back-reflection x-ray patterns made with the test plane parallel with the x-ray film and normal to the x-ray beam. The position of the long axis of the indentation must be noted with respect to the top or other mark on the x-ray film at the time of setting up for the diffraction pattern; otherwise θ may be lost. In hexagonal and tetragonal crystals, the extinction angle may be measured by polarized light to determine θ, provided the specimen is transparent and in a suitable mounting.

     THE KNOOP MICROHARDNESS TESTER TABLE 1. LIMITS OF VARIATION OF φ AND ρ RESULTING FROM CRYSTAL SYMMETRY

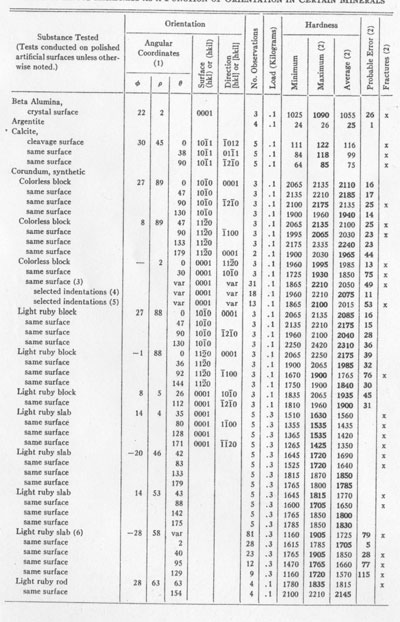
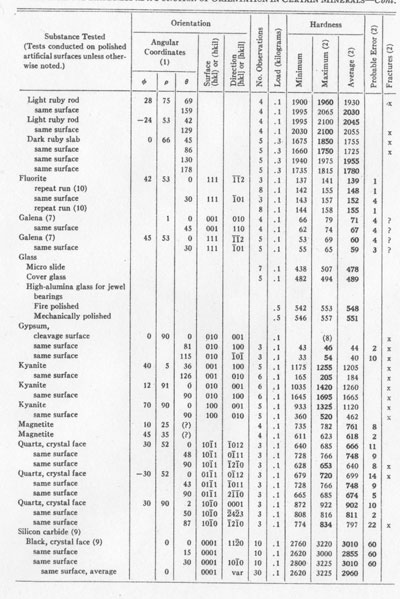
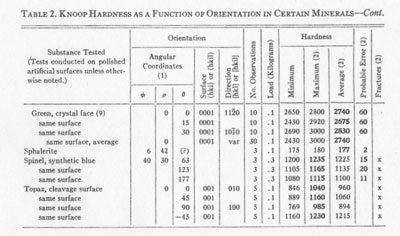
     TABLE 2. KNOOF HARDNESS AS A FUNCTION OF ORIENTATION IN CERTAIN MINERALS

NOTES TO TABLE 2

     (1) Angular coordinates are as defined in Fig. 3 and as measured by means of x-ray diffraction patterns

     (2) In the column headed Fractures is indicated the presence of small fractures observed about the marks of the indenter. If fractures were present, the maximum hardness reading of a series is considered the best, and is so indicated by boldface numerals, but if no fractures were observed, the average is considered the best value obtainable from the series, and is so indicated by the same means. The probable errors were calculated for the maximum or for the average, whichever is considered best value.

     (3) Indentations in 31 different directions.

     (4) Selected indentations with no fractures.

     (5) Selected indentations with minor fractures.

     (6) Combined results from the following four items.

     (7) No fractures visible, but fractures probable on account of the excellent cleavage.

     (8) Large fractures; measurements impossible at lightest available loads (0.1 Kg).

     (9) Probable errors for silicon carbide observations are approximate.

     (10) Original measurements August, 1942. Repeated January, 1945, because of question raised by comparison with published results (Table 3), and to observe effect of addition of magnetic device for preventing indenter-overload due to impact.

    RESULTS OF TESTS

     Table 2 contains the collected results of mineral hardness determinations made at the Hamilton Watch Company laboratories over a period of approximately 3 years. Bearing in mind the rather academic importance of most of these results, the reader will understand why more extensive tests cannot easily be made here. This list does include a wide enough variety of minerals and mineral-like materials to indicate very promising possibilities for application of the Knoop indenter to determinative mineralogy and to crystallography. Several type-minerals in Mohs' scale, and some in the scale of hardness of Talmage (1925), are included in Table 2. It should be emphasized that determinations from fractured indentations marked "x" were of a reduced order of accuracy because of the fractures. Such determinations should not be considered final nor necessarily even approximately accurate; they are the best we have available, however, and it will be noted that even in spite of the uncertainty introduced by the presence of fractures, the fractures themselves appear to have been fairly consistent for any given orientation, and the readings therefore were fairly constant. Analysis of the table will show that the largest probable error for a good determination is less than 5% of the hardness number.

     It is especially to be noted that most of the substances tested in several orientations showed considerable variations of hardness with orientation. The well-known variation of scratch-hardness with scratch direction on the macropinacoid of kyanite is reflected by variations obtained by indenting that surface with the indenter either parallel to, or at right angles to the direction of the c-axis. If we consider the direction of scratching and the azimuth of the indenter for the highest hardness value observed on the surface tested, we note a discrepancy as follows:

     Azimuth (B) for maximum hardness in kyanite

    3 If n observations of a quantity are represented by x₁, x₂, ······, x_n, and their mean by x(bar), and their respective deviations from x(bar) by d_i, then the probable error of any individual observation is 0.6745(Σd²_i/(n-1))^1/2 and the probable error of the mean is  0.6745(Σd²_i/n(n-1))^1/2.