Screw dislocations

Home	AmMin	GMR	RiMG	Collectors Corner	Directory	Short Courses

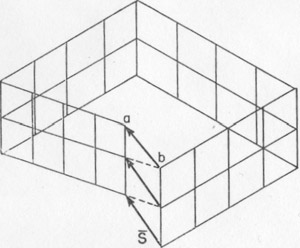
Volume 40, pages 139-146, 1955

SCREW DISLOCATIONS AND CHARGE BALANCE AS FACTORS OF CRYSTAL GROWTH¹

STERLING B. HENDRICKS, U. S. Department of Agriculture, Plant Industry Station, Beltsville, Md.

Screw dislocations in crystals are discussed and the growth spirals that arise from them are illustrated. A second general method of crystal growth is advanced. It depends upon the necessity of balancing the forces between ions or atoms at terminating crystal surfaces.

The importance of screw dislocations for crystal growth was stated by F. C. Frank at the symposium on "Crystal Growth" of the Faraday Society in 1948 (8, 9). This was soon followed by striking experimental verification (10, 1). Thus has opened a subject with many consequences in crystallography.

Frank's deduction was essentially of two parts. First, the observed rates of crystal growth at low supersaturation are too rapid to be explained by nucleation on flat surfaces (9). Second, growth can take place at the observed rate at the intersection of two surfaces in the reentrant angle of the surface step generated by emergence of the Burgers vectors. The background for this second deduction follows.

That the elastic strain of any rigid body can be resolved into six components with associated displacements was developed by V. Volterra in 1907 (13) and further formalized by A. E. H. Love in 1927 (11) who introduced the term "dislocation" in place of "distortioni" as used by Volteria. One of these six components of strain was shown by J. M. Burgers in 1939 (6) to be of the type shown in Fig. 1. In this figure the circuit, which is a path for integration, can be considered to be in the elastically deformed material surrounding an imperfection in a crystal (dislocation). Upon passing from a to b by a succession of primitive lattice translations, there is an error of closure represented by the vector s{bar}. This vector, the Burgers vector or screw, displacement, must be a vector sum of the elastically strained primitive translations of the lattice.

FIG. 1. The Burgers vector s{bar}. The indicated circuit by primitive translations of the lattice is in elastically strained material around a dislocation.

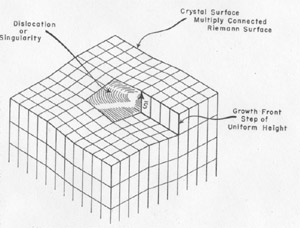
The Burgers vector s{bar} is conserved along a cylinder which either must be closed upon itself, as a torus, for instance, or intersect the surface since, otherwise, the line integral of the elastic strain could not be conserved. Thus, a screw displacement of the lattice points on the surface can be generated. The entire volume of the crystal can develop by increments of growth about the screw axis without requiring fresh two dimensional nucleation. Conversely, the screw displacement is evident on a final crystal surface as a step, on a cleavage surface of mica, for instance, or as a spiral if lateral growth has taken place.

A screw displacement on a crystal surface is illustrated in Fig. 2. The surface is continuously warped such that as the growth front advances, clockwise in the illustration, by accretion of new material a helix of pitch s{bar} is generated. In the center region the crystal is not defined; here the strain exceeds the elastic limit. This center region is the nucleus for crystallization as well as the region where etching starts. It has been observed to have a diameter as great as 35 microns (in biotite) and probably always exceeds many units of structure.

The growth spirals or helices are readily observed and have been described as found on many crystals (9, 2, 5). They generally can be seen at moderate magnification (say 200) and can be measured precisely by multiple beam interferometry. Several or many Burgers vectors might emerge on a crystal surface. In this case, they can interact to give figures in which the spiral character is not immediately evident (2). A simple case is where two screw displacements are of equal pitch but opposite rotation as shown in Fig. 3. Then a succession of closed loops are present which spread outward as the crystal grows. An example of interaction between three growth spirals, taken from the work of S. Amelinckx (2), is reproduced as Fig. 4.

FIG. 2. A step on a crystal face arising from a screw dislocation which gives a growth front for extension of the crystal as a Riemann surface generated by the spiral.

FIG. 3. Interaction of two spirals of equal s{bar} but opposite rotation. A single spiral is shown on the right (SiC, courtesy W. Dekeyser and S. Amelinckx).

Growth on screw dislocations not only serves to account for observed rates of crystallization but also to perserve unusual sequences of layer succession in crystals having layer structures such as micas, SiC, graphite, etc. This was pointed out by S. Amelinckx and W. Dekeyser (5) for micas. In the polytypic polymorphism of these crystals there is a succession of layers, the individual arrangements of which can be represented by, say, A, B, and C. Thus, cubic close packing is ABC ABC-while hexagonal close packing is ABABAB--. Possibilities exist for other sequences such as ABC ABAC ABC ABAC -- and some have been observed. Prior to the discovery of screw dislocations, presence of such layer sequences seemed to imply interaction over long distances for repetition. But now it is evident that the repetition is preserved by the screw dislocation and that the repetition distance of the lattice is the pitch of the screw, or the displacement s{bar} (5). In this way, too, might arise an orderly sequence of layers of different composition such as chlorite-mica-chlorite-mica -- or vermiculite-mica-vermiculite-mica-of types which have been observed.

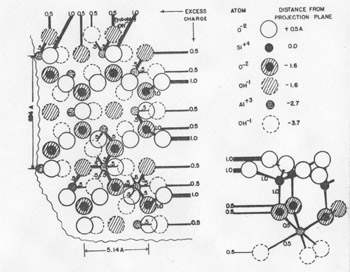
FIG. 4. Interaction of three growth spirals (schematic), two clockwise and one counterclockwise (after S. Amelinckx).

Growth of hopper shape crystals at liquid surfaces are also readily explained (4). In fact, observation of the growth spirals is very simple in such cases and those appearing on K₄Fe(CN)₆ or salol can be used for student demonstration experiments.

The very elegance of this advance and the extensive occurrence of screw dislocations in crystals, however, raise the danger that screw dislocations will be considered the only site of crystal growth at low supersaturations. Frank has avoided this implication, but Seitz (12), in an incidental discussion to a main purpose (essentially as an appreciation), states: "Frank has pointed out that dislocations catalyze crystal growth so that an otherwise perfect crystal containing dislocations should grow far faster than one that does not. In fact, Frank's analysis shows that the presence of dislocations is almost a necessity for growth of crystals by vapor deposition or from solution in periods of time of every day or even geological interest." There is negative evidence, which truly might be only lack of observation, against the statement in the second sentence in that growth spirals have not been found on many crystals (calcite, sodium bromide) upon careful examination.

Actually, there is another general process for growth at low supersaturation and it is this process that is called "charge balance" in the title, a choice of term that might be none too happy. The process is really a result of Pauling's principle of microscopic neutrality (Electrostatic Valence Principle) which recognizes that in ionic crystals neutrality of surroundings is maintained among the immediate neighbors of an ion. Thus, a crystal containing silicate groups or any groups of atoms such as CO₃^--, SO₄^--, etc. brings up a more serious question of termination than of growth. Growth is by a leap-frog type process in which accretion of negative ions requires added positive ions which, in turn, requires further negative ions, etc. for charge balances. Nor is the process restricted to ionic substances, but might be expected in any case where the atomic arrangement is involved.

This process of growth was perhaps sensed by H. E. Buckley (7) who in discussing failure of concepts of theories of perfect lattices as controlling crystal growth developed by Kossel and Stranski, among others, points out: "Another difficulty arises because, so far, the problems in the calculations of crystal-surface force fields are so great that simplifying assumptions have to be made to render them capable of any solution at all. Such, for example, is that of assuming that ions to be spherically symmetrical (an assumption probably near the truth for rock salt ions). But to what extent can the consequences derived from these simplified cases be applied to more complex crystals with RO₄ ions, of perhaps not even regular tetrahedral shape?"

The lack of charge balance of an (hk0) face of kaolinite is shown in plan and elevation in Fig. 5. The impossibility of both balancing the charge at the face and terminating the crystal without changing the structure from that of kaolinite can be appreciated. This difficulty can only be met by the presence of exchangeable ions and thus the surface differs in composition from the interior. But even the presence of these external ions would not prevent the charge pattern on (hk0) from serving to continue growth.

The failure of charge balance at an (hk0) surface of kaolinite essentially illustrates the situation for the structurally related micas. Growth spirals have been observed on the cleavage plane (001) of biotite (5) and these, in general, probably account for the addition of structural layers. But the crystals usually are thin, which implies that the lateral growth is more rapid than that normal to (001). In principle, this could be due to growth. on screw dislocations on (hk0), but upon closer examination such an explanation is very improbable as new layers would have to be initiated as the growth front progressed. Actually, growth on the fronts of the screw dislocations on (001) probably does not depend upon accretion at the reentrant angle, but rather over the entire front by the requirement of charge balance. In fact, the reentrant angle loses significance when considered on an atomic scale.

FIG. 5. Charge excess on an (hk0) termination of kaolinite shown in plan and elevation. Growth is enhanced by the difficulty of balancing the charge.

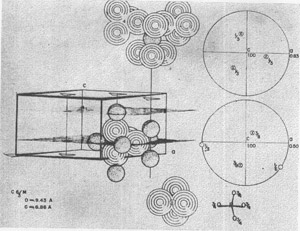
Apatite, Ca₁₀(PO₄)₆F₂, might serve as a further example for discussion. Growth spirals have been observed on (1010) and, in fact, the crystal habit probably often results from the shape of the spirals (3). The atomic arrangement on (1010) is partially shown in Fig. 6. The difficulty of termination is precisely that mentioned by Buckley, for the multiply-charged tetrahedral PO₄^--- requires arrangements of Ca⁺⁺ ions that can only be met by adding further PO₄^--- ions. In a more formal way, this is shown by the stereographic projection for the components of electrostatic valence around a Ca⁺⁺ ion on a three-fold axis and of an oxygen atom on a reflection plane. The growth then might be at the spiral front by the balancing of charge on this front.

FIG. 6. Atomic arrangement on a (100) termination of apatite. The stereographic projections show the electrostatic valence distribution around Ca⁺⁺ on a three-fold axis and oxygen of a PO₄^--- group on the reflection plane.

Growth of alkali halide crystals are of interest in the bearing on both screw dislocations and balance of charge - or rather potential balance. Growth spirals have been observed on NaCl crystals and these crystals readily form in hopper shapes. If (100) is considered as a terminating surface, the charge distribution is balanced since at (100)₀ and (100)_1/2 Na⁺ and Cl^- are equivalently surrounded and thus would not serve for continued growth. But as the size of the negative ion is increased, as in NaBr, this ion deviates from being essentially a point charge. In such crystals the detailed balancing at the surface could be important for continuing growth.

ACKNOWLEDGMENT

Frank's first publication on growth spirals in the Transactions of the Faraday Society in 1949 was a striking example of deduction, but I did not comprehend the wide implications until reports of observation on many crystals shortly began to appear. Among these were numerous examples due to Prof. W. Dekeyser and Dr. S. Amelinckx of the Laboratorium Voor Kristalkunde, Geologish Instituut, University of Ghent, Ghent, Belgium. I spent a short time in Ghent in September, 1954, discussing the phenomena and in making some of the simpler observations and measurements with the guidance of Dr. Amelinckx. Photographs from which Fig. 3 was selected were supplied by Prof. Dekeyser and Dr. Amelinckx. The effect of charge balance on crystal growth was also raised with Prof. Dekeyser and the example of sodium bromide was suggested by him. The concept seemed already to be part of his thinking and it might well have been stated some place in the older literature.

REFERENCES

1. AMELINCKX, S., Nature, 167, 939 (1951); 168, 431 (1951), Jour. de China. Plays., 48, 425 (1951).

2. AMELINCKX, S., Jour. de China. Phys., 49, 411 (1952).

3. AMELINCKX, S., Nature, 170, 760 (1952).

4. AMELINCKX, S., Jour. de China. Phys., 50, 218 (1953).

5. AMELINCKX, S., AND DEKEYSER, W., Cong. Geol. Int. Algiers, 1952, 18, 9 (1953).

6. BURGERS, J. M., Proc. Acad. Sci., Amsterdam, 42, 293 (1939); 42, 378 (1939).

7. BUCKLEY, H. E., Crystal Growth, John Wiley & Sons, New York (1951), p. 178.

8. FRANK, C. F., Discussions of the Faraday Soc., 5, 48 (1949).

9. FRANK, F. C., Advances in Physics, 1, 91 (1952).

10. GRIFFIN, L. J., Phil. Mag., 41, 196 (1950).

11. LOVE, A. E. H., The Mathematical Theory of Elasticity, Cambridge Univ. Press (1927).

12. SEITZ, F., Imperfections in Nearly Perfect Crystals. John Wiley & Sons, New York (1952), p. 40.

13. VOLTERRA, V., Ann. Ecole Norm. Super., 24, 400 (1907).

NOTE

1 Address, in part, of the retiring President of the Mineralogical Society of America, given at the thirty-fifth meeting of the Society in Los Angeles, California, November 2, 1954.